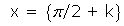Matematicas 4: mayo 2013

APLICAS FUNCIONES PERIODICAS

Es una función cuya representación gráfica se repite a intervalos regulares. Esta propiedad las hace muy útiles para entender la multitud de fenómenos periódicos que se dan en nuestro mundo. el día, la noche, las olas del mar, los látidos del corazón, el movimiento de la cuerda en una guitarra, todos ellos son ejemplos de fenómenos periódicos. Su estudio matemático se hizo posible gracias al uso de las funciones seno y coseno. Empecemos a tratar de responder la pregunta:

¿Qué es una función periódica?

Si ahora son las 16 hs, en punto, ¿ que hora será dentro de 24 hs ? ¿Y que hora será dentro de 48 hs? ¿Y que hora será dentro de cualquier múltiplo de 24 hs? El ciclo en este caso es de 24 horas. En estos ejemplos supondremos que la hora la contamos de 0 a 24 hs y no de 0 a 12 hs.

La función "que hora es" es una función periódica, cuyo período es de 24 hs. ¿Cómo será la representación gráfica de la función "que hora es" ? Vamos a investigar.

Trata de hacer la gráfica tomando un intervalo de tiempo de 60 horas. En el eje de las abscisas ubicamos el tiempo, y en las ordenadas, h(t) , que es la función del tiempo "que hora es (t)". La podemos abreviar llamándola h(t). Podemos tomar el tiempo inicial como una hora cualquiera, por ejemplo las 10:00.

h(0) = 10 Es la hora inicial.

Dentro de una hora serán las 11 hs. En lenguaje matemático, h( 1) = 11.

Dentro de 8 horas serán las 18 hs. En lenguaje matemático, h(8) = 18

Dentro de 24 hs serán de nuevo las 10 hs: h(24) = 10

Dentro de 2 días, o sea, 48 horas, serán otra vez las 10hs. h(48) = 10

Esta función es periódica porque en t=0, 24, 48, ...... tiene "el mismo valor".

Recordemos que la función h(x) es periódica porque en t=0, 24, 48, ...... tiene el mismo valor.

Entonces h es periódica, porque existe un número real p=48 tal que verifica que h(t)=h(t+48) para cualquier número t.

h(7)=h(7+48)=h(55) Esto está diciendo que "la hora" dentro de 7 horas será la misma que dentro de 55 horas.

Pero ya habrás notado que 48 no es el menor número que tiene esa propiedad. Hablando de horas, el menor número que tiene esa propiedad es el 24. Recuerda que estamos hablando de la hora en formato de 0-24 y no de 0-12.

Definición: Una función f es periódica, si existe un número real p tal que verifica . Llamaremos período al mínimo p.

p tiene que ser el mínimo, porque si no lo definimos asi, si f es periódica de período p, entonces f tambien sería periódica de período 2p, 3p, 4p, .....y tendríamos infinitas definiciones de período.

Propiedad: La representación gráfica de las funciones periódicas es una curva que se repite en cada tramo de longitud p.

Las funciones seno, coseno y tangente , cuyas imágenes anotaremos sen(x), cos(x) y tg(x) , son ejemplos de funciones periódicas.

Pero mucho cuidado, que no todas las funciones periódicas tienen que ser sinusoidales. Ya vimos ejemplos, como el de "la hora", que hay muchísimas funciones periódicas, en realidad, infinitas, que no tienen nada de seno ni de coseno.

Pero aunque no todas las funciones periódicas tienen algo de seno o de coseno, lo cierto es que las funciones seno y coseno son unas de las mas importantes en lo que respecta a funciones periódicas.

La función seno

Se denomina función seno, y se denota por f (x) 5 sen x, a la aplicación de la razón trigonométrica seno a una variable independiente x expresada en radianes. La función seno es periódica, acotada y continua, y su dominio de definición es el conjunto de todos los números reales.

Gráfica de la función seno.

La función coseno

La función coseno, que se denota por f (x) = cos x, es la que resulta de aplicar la razón trigonométrica coseno a una variable independiente x expresada en radianes. Esta función es periódica, acotada y continua, y existe para todo el conjunto de los números reales.

Gráfica de la función coseno.

Propiedades de las funciones trigonométricas

Como características importantes y distintivas de las funciones trigonométricas pueden resaltarse las siguientes:

Las funciones seno, coseno son de naturaleza periódica, de manera que el periodo de las funciones seno y coseno es 2p .
Las funciones seno y coseno están definidas para todo el conjunto de los números reales. Ambas son funciones continuas.
Las funciones seno y coseno están acotadas, ya que sus valores están contenidos en el intervalo [-1,1].
La funcion seno es simétrica respecto al origen, ya que sen (-x) = -sen x; . En cambio, la función coseno es simétrica respecto al eje Y: cos (-x) = cos x.

Funciones circulares recíprocas

Se llaman funciones circulares recíprocas a las que anulan la acción de las funciones trigonométricas. A cada función trigonométrica le corresponde una función circular recíproca, según la relación siguiente:

La función recíproca del seno es arco seno, simbolizada por f (x) = = arc sen x.
La función recíproca del coseno es arco coseno, expresada por f (x) == arc cos x.

Función seno tiene la siguiente forma:

y = A sin[ω(x - α)] + C

A es la amplitud (la altura de cada máximo arriba de la línea base).
C es el desplazamiento vertical (la altura le la línea base).
P es el periodo o longitud de onda (el longitud de casa ciclo).
ω es la frecuencia angular, y se expresa por
ω= 2π/P o P = 2π/ω.
α es el desplazamiento de faso.
Función coseno tiene la siguiente forma:

y = A cos[ω(x - α)] + C
- A es la amplitud (la altura de cada máximo arriba de la línea base).
- C es el desplazamiento vertical (la altura le la línea base).
- P es el periodo o longitud de onda (el longitud de casa ciclo).
- ω es la frecuencia angular, y se expresa por
  ω= 2π/P o P = 2π/ω.
- α es el desplazamiento de faso.
Ejemplos
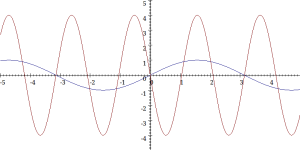
Considere la siguiente gráfica, que muestra una curva de seno "general" (desplazada y escalada):
Pregunta ¿Que es la ecuación de la gráfica?
Contesta Consultando la función seno generalizado a la izquierda, vemos que la ecuación de esta curva es:
donde
- La línea base (el punto medio de oscilación) se ubica 2 unidades abajo del eje x
- A = amplitud (la altura de cada máximo arriba de la línea base) = 2
- C = desplazamiento vertical = coordenada y de la línea base = -2
- P = periodo (el longitud de casa ciclo, o distancia de un máximo al siguiente) = 4
- ω = frecuencia angular = 2π/P = 2π/4 = π/2
- α = desplazamiento de faso = 1 Esta es la distancia horizontal del eje y al primero punto donde la gráfica cruza la línea base.
Entonces, la ecuación de la curva más arriba es
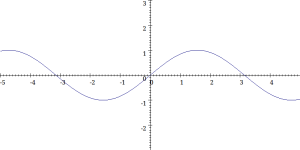
Las funciones trigonométricas son periódicas, es decir que cumplen con

$f(x) = f(x + P) \; \forall x \in Dom(f)$

En donde $P$ es el periodo. El seno, coseno y sus inversas tienen $P = 2 \pi$ ; la tangente y la cotangente tienen $P = \pi$ .

Ejemplo 5.1: ¿Cual es el periodo de la función $\displaystyle {y = 15sen \left(\frac{\pi x - 4}{2} \right)}$ ?

Quiero $P$ tal que $f(x) = f(x + P)$ . Es decir

$\displaystyle {15sen \left(\frac{\pi x - 4}{2}\right) = 15sen\left(\frac{\pi (x+P) - 4}{2}\right)}$

Y sabemos que el periodo del coseno es de $2 \pi$

$\displaystyle {15sen \left(\frac{\pi x - 4}{2}\right) = 15sen\left(\frac{\pi x - 4}{2}+2\pi\right)}$

Por lo que

$\displaystyle {15sen\left(\frac{\pi (x+P) - 4}{2}\right)= 15sen\left(\frac{\pi x - 4}{2}+2\pi\right)}$

Así que lo que quiero es que

$\frac{\pi (x+P) - 4}{2} = \frac{\pi x - 4}{2}+2\pi \Rightarrow \pi x + \pi P - 4 = \pi x - 4 + 4\pi \Rightarrow P = 4$

En general, en una función de la forma $y = sen(\omega x + \phi)$ el periodo es $\displaystyle {\frac{2 \pi}{\omega}}$ . (Lo mismo vale para el coseno, pues el coseno coincide con el seno si se lo desplaza $\frac{\pi}{2}$ ). $\omega$ es lo que se llama la frecuencia angular, que se define como

$\displaystyle { frecuencia \; angular = \frac{2\pi}{periodo}}$

Función seno

f(x) = sen x

Propiedades de la función seno

Período: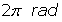 Recorrido

recorrido: [−1, 1]

Mínimos: 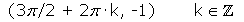Máximos:

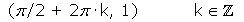Cortes con el eje OX: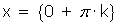

Función coseno

f(x) = cosen x

Propiedades de la función coseno

Período: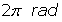 Recorrido: [−1, 1]

Mínimos:

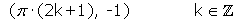maximos:

Cortes con el eje OX: